Era uma vez, uma cônica chamada Elipse. Tinha uma beleza própria que, no entanto, não era apreciada pela maioria. A Elipse teve filhas. Ninguém sabe ao certo quem foi o pai, mas uma delas, a Circunferência, ganhou muita fama. Só falavam dela e de como ela era perfeita.
A beleza da Circunferência encantava a todos. Na verdade, ela era a própria definição de beleza: “um somatório de partes que funcionam juntas, de tal forma que nada precisa ser retirado, acrescentado ou alterado”.
A Circunferência era uma forma idolatrada.
Mas, afinal, ela não era realmente perfeita, senão aos olhos míopes de seus admiradores. Quem conseguia ver além da curva, seria capaz de perceber que sua mãe, a Elipse, era mais verdadeira.
Bastava abrir os olhos. A Elipse estava por toda parte. Pertencia à natureza. A Circunferência, ao contrário, era ilusória. Onde se achava que a encontraríamos, lá estava, na verdade, outra Elipse. A Circunferência só existia se fosse fabricada de propósito. E a natureza dificilmente faz isso.
Ainda hoje há muitos que amam a forma idealizada da Circunferência, como se ela fosse única no mundo. Eles ainda não descobriram a verdade: que o objeto de sua obsessão não passa de um caso da Elipse…
Uma curva, dois centros
Elipse é um conjunto de pontos de um plano cuja soma das distâncias a dois pontos fixos nesse plano é sempre a mesma. Ok… É melhor desenhar.
Na figura ao lado, você pode (deve!) mover os pontos P, F e G. Repare que a soma dos segmentos FP e PG é sempre a mesma. Ao mover esses pontos você obtêm diferentes formas. Todas são elipses.
Mesmo quando você faz o ponto F coincidir com o ponto G a definição destacada acima continua valendo. Só que nesse caso, chamamos a figura resultante de circunferência.
Sim! A circunferência é um caso particular da elipse, quando seus dois centros se fundem num só.
Outro caso particular é quando você afasta tanto os pontos F e G um do outro que P é puxado para a linha que os contêm. Nessa situação bizarra, dizemos que a elipse degenerou num segmento de reta.
A propósito, os centros de uma elipse são chamados de focos. E o motivo para isso tem a ver com o que podemos fazer com eles…
Elipses na natureza
Há elipses por todo Universo. Planetas se movem em torno de suas estrelas em órbitas elípticas. Luas em volta de planetas. Cometas, asteroides e toda sorte de corpos celestes trafegam em órbitas com formato de elipse. Algo tão comum que virou , formulada pelo astrônomo e matemático alemão Johannes Kepler (1571-1630).
A elipse tem uma propriedade muito interessante – e de uso bastante prático.
Se um raio de luz ou uma onda sonora emanar de um dos focos, ele será refletido direto para o outro. De um centro da elipse para o outro – e é por isso que eles são chamados de focos.
Essa propriedade é usada para criar “cochichôdromos” – estruturas elípticas que permitem que alguém que apenas sussurre em um foco seja ouvido claramente por uma pessoa no outro foco, mas não por quem estiver entre eles (figura ao lado).
Não é apenas uma curiosidade divertida. Isto é usado num método clínico chamado Litotripsia, na qual um paciente com cálculo renal pode fragmentar as pedras usando um aparelho que alinha seus rins num dos focos de uma elipse. No outro, ondas de choque emanam para se concentrar no cálculo renal, reduzindo-o a fragmentos tão pequenos quanto areia, sem cirurgia e sem desconforto.
Figura excêntrica
Uma elipse é sempre uma elipse, mas nem por isso elas são todas iguais. Assim como nós, as elipses podem ter vários “rostos”, uns mais, outros menos alongados.
Quanto maior a distância entre os focos, mais alongada será a elipse. Quando mais eles se aproximam, mais ela se arredonda. O que define o arredondamento ou achatamento de uma elipse é uma relação chamada excentricidade – palavra que significa “distanciamento do centro”.
A excentricidade da órbita da Terra ao redor do Sol mede 0,017. Vendo o desenho (abaixo), qualquer pessoa diria se tratar de uma circunferência. Mas não é. É uma elipse!
A excentricidade varia entre zero (uma circunferência) e 1 (um segmento de reta). Portanto, todas as elipses vão ter valores de excentricidades maiores que zero e menores do que 1. As possibilidades são infinitas.
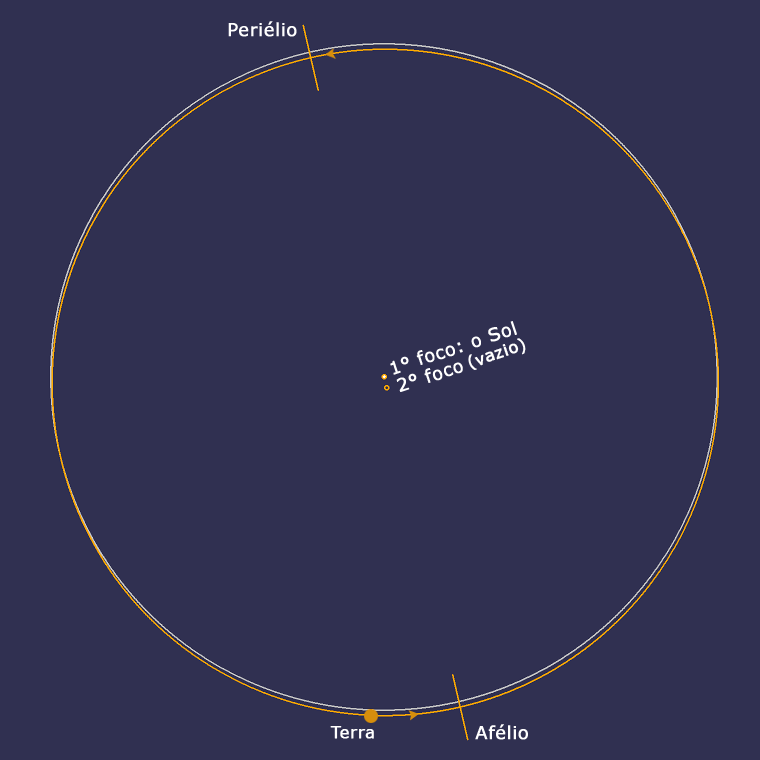
DISSIMULADA A órbita da Terra é uma elipse (acima, em amarelo) com quase 300 milhões de km em seu eixo maior (entre Afélio e Periélio). Mas os focos estão separados por meros 5 milhões de km (cerca de 4 vezes o diâmetro do Sol). Por isso é tão difícil distinguí-la de uma circunferência (em azul). Adaptado de Wikimedia Commons.
No Sistema Solar, a órbita planetária mais excêntrica é a de Mercúrio (0,205). Cometas têm órbitas ainda mais alongadas. O de Halley, por exemplo, tem 0,967 de excentricidade orbital.
É possível manter um satélite artificial numa órbita circular. Mas bastará uma pequena alteração em sua velocidade e ele mudará seu caminho para uma trajetória elíptica. Como há uma quantidade infinita de órbitas elípticas possíveis, a órbita perfeitamente circular torna-se um caso bastante improvável.
Órbitas com formato de elipse são estáveis. Quando a Terra está mais próxima do Sol viaja mais rápido, indo mais devagar quando está mais longe. A média é equivalente a uma órbita circular, sem a necessidade de um ajuste preciso de velocidade o tempo todo. A natureza não gasta energia à toa.
Construa sua elipse
As curvas geradas na intersecção de um plano que atravessa um cone são chamadas de cônicas. Elipse, parábola e hipérbole são os três tipos de cônicas que podemos obter por esse processo.

HORA DA SEÇÃO Quando um plano corta um cone, temos as cônicas! À esquerda, a parábola. No centro, a elipse e seu caso particular, a circunferência. À direita a hipérbole. Fonte: Wikimedia Commons.
Uma das formas mais simples de desenhar uma elipse é utilizando alfinetes ou tachinhas para marcar seus focos e fixando neles um pedaço de barbante, com folga. Um lápis ou caneta é então utilizado para dar a volta nos focos mantendo o barbante esticado. Esse método é geralmente conhecido como “elipse do jardineiro” e pode ser simulado abaixo.
As cônicas (ou seções cônicas) têm sido estudadas desde a Antiguidade por matemáticos e astrônomos como o grego Apolônio de Perga, que viveu por volta do ano 200 AEC. Mas sem dúvida foi o trabalho de Johannes Kepler, no século XVII, que tornou a elipse célebre entre os astrônomos.
Estudando a órbita de Marte, Kepler primeiro tentou ajustá-la num círculo, pois, afinal, ele também considerava a circunferência uma figura perfeita, até divina. Mas os dados observacionais não batiam. Então, ele tentou uma oval. Melhorou um pouco, mas não o suficiente. Foi quando Kepler decidiu usar a elipse que tudo se encaixou.
“Todos os planetas se movem em órbitas elípticas, com o Sol em um dos seus focos”, foi o que postulou sua primeira lei, a Lei das Órbitas (Astronomia Nova, 1609). Kepler, enfim, foi capaz de enxergar a verdadeira forma das órbitas – e a beleza que só a elipse podia ter. ![]()
+ A superlua
+ Desvendando a órbita de Mercúrio



